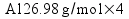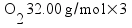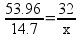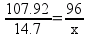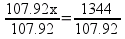I’ve often said to students that I’d rather be taking an exam than grading one. They sometimes stare back at me with jaws hanging open, shocked that I would say such a thing. In this post, I thought I’d take a brief look at a few of the reasons why grading an exam is harder than taking one.
Here’s a question from one of my recent exams for an introductory chemistry course.
Metallic aluminum (Al, FW = 26.98 g/mol) reacts with oxygen gas (O2, FW = 32.00 g/mol) to produce aluminum oxide (Al2O3, FW = 101.96 g/mol). How many grams of oxygen gas are required to react with 14.7 grams of aluminum metal?
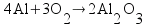
Based on the way I taught my students to solve this sort of problem in class (the factor-label method), I expected most students to come up with the answer 13.1 g of O2 using a calculation procedure similar to this one:
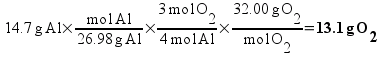
But there’s a hitch! There’s more than one way to work this problem. Another way to solve the problem is to find out the mass ratios of aluminum to oxygen based on the chemical equation and set it up as a ratio:
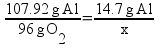
Solving, x = 13.1 g of O2.
This looks very different than the first way I showed to solve the problem. Though it’s not the way I taught chemical calculations, it’s a perfectly legitimate strategy for solving this kind of problem. To make it more … interesting, you can actually set up the ratios so that they look a little different from the way I wrote them above.
So, when you prepare to grade a test, you not only have to solve the problem the way you would have solved it yourself, but you also have to consider the problem-solving strategies your students might come up with to solve the problem. Otherwise, you won’t be able to see whether a student actually has an understanding of the material, and you won’t be able to help them correct any mistakes they made if you aren’t able to follow their strategies.
Think that’s bad? There’s another hitch!
Here is an actual student answer to the problem above.
8.72 g of O2 is needed to react with 1.47 g Al
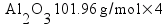
107.92 Al
96 O
53.96x = 440.4
8.7214.7g Al = ___________ g O2
12.45
(Yes, the answer really did look like that on paper.)
Obviously, the student got the wrong answer. Equally obviously, this “solution” is a mess! But, is there anything we can work with here in the mess? Is there any help we can give the student so that (s)he might do better next time?
It’s very clear that the student wanted to try using the ratio method to solve the problem. Why? There are actually two attempts to use the ratio method in this answer. The attempt on the right would have actually gotten the student to the right answer, but the student makes a math error in the attempt and comes up with 12.45 g of O2. Because the student doesn’t label what their numbers or letters represent, (s)he simply doesn’t realize that the value of x is the desired answer – and gets lost.
Once students start floundering in a sea of unfriendly numbers, they never end up anywhere useful. The wrong-on-all-counts ratio on the left-hand side of the page makes that point quite clearly. If the student had reazlied that the value of x in the ratio on the right was the desired answer, (s)he would have stopped at 12.45 g O2. Still not correct, but only off because of a case of fumble-fingers with the calculator.
The advice this student needs to hear, I think, is that when solving a problem it is vitally important to keep track of what numbers and variables actually represent. In math class, students find x for x‘s sake. Everywhere else, x is merely a name for sometihng real. This is a point that I don’t think is made nearly strongly enough in math classes.
But back to the title of this post – how long did it take to sift through the student answer? Longer, i’d wager, than the student spent on the exam solving the problem. And that’s why grading an exam is harder than taking one!